Tenor clef

The tenor clef determines the position of the C note on the staff (stave ):



From this reference, all others music notes will be placed before and after the C note:

What instruments use the tenor clef?

The tenor clef is used by the following instruments:

Strings instruments:
- Cello (in the high register)
- Double bass (in the high register)

Brass instruments:
- Trombone (in the high register)

Woodwind instruments:
- Bassoon (in the high register)

The tenor clef for transposition (players)

The tenor clef is also used for the transposition by some players and conductors:

Imagine you are a horn player (and you are very lucky to play this instrument ) and you want to play the sheet music of an alto saxophone. The horn is in F and the alto saxophone in E flat, so you will have to lower each note by one whole step (tone ), this is like playing the saxophone score with a tenor clef instead of a treble clef:



To transpose at sight from E♭ to F, the horn player mentally replaces the treble clef by a tenor clef and must also add two flats.

Key signatures in tenor clef

Here are positions of flats and sharps in the key signature on the staff with a tenor clef:

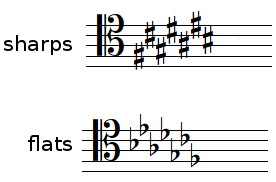
Example of the use of the tenor clef for the cello

Usually cellists read music with a bass clef, but when the music notes get too high, then there are too many ledger lines above the staff (extra lines), and it is very usefull to use the tenor clef instead. Here is an example in the Poco allegretto movement from Brahms' Symphony No.3 Opus 90:

This royalty-free sound sample was recorded in 1936 by the Vienna Philharmonic Orchestra conducted by Bruno Walter (source, Attribution-Noncommercial-Share Alike 3.0). You will also notice the use of an anacrusis.

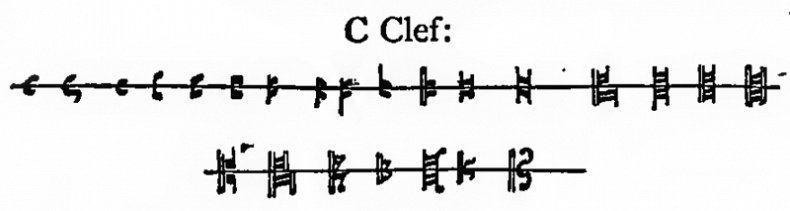
Evolution of the C-clef symbol

In the book A history of music by Charles Villiers Stanford and Cecil Forsyth, a representation of the evolution of the C-clef clef symbol is exposed (source):

Learn to read tenor clef

Here is a game to learn tenor clef notes: