An interval is the inclusive distance between two music notes. An interval can be melodic or harmonic.
Each melodic or harmonic interval has a number and a quality, we will see this later.
Melodic interval
A melodic interval is an interval in a melody when notes are played one after the other:

Harmonic interval
An harmonic interval is an interval between two notes in the same chord, when notes are been playing at the same time:

Melodic motions
Melodic motions can be conjunct or disjunct:Conjunct melodic motion
When 2 notes follow each other, then it is a conjunct melodic motion:
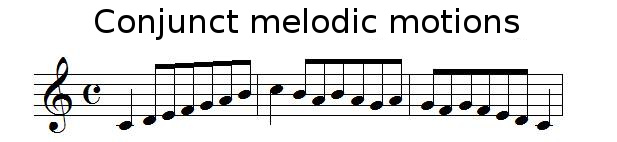
(Conjunct melodic motions can be ascending or descending)
Disjunct melodic motions
When 2 notes do not follow each other, then it is a disjunct melodic motion:
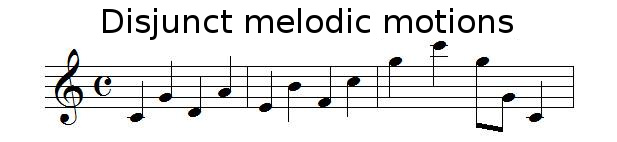
(Disjunct melodic motions can be ascending or descending)
Number of an interval
Each interval has a number that is the number of letter name it contains.
List of interval numbers
- 1 Unison
- 2 Second
- 3 Third
- 4 Fourth
- 5 Fifth
- 6 Sixth
- 7 Seventh
- 8 Octave
- 9 Ninth
- 10 Tenth
- 11 Eleventh
- 12 Twelfth
- 13 Thirteenth
.. ......
.. ......
and so on
For example, if you consider the interval starting from C and ending on G, you must count like this: C-D-E-F-G = 1-2-3-4-5, so this interval is a fifth (5th).
The unison is a null interval, that is to say that the 2 music notes of a unison intervall have the same sound.

Ascending and descending intervals
An interval can be ascending or descending:

Interval quality
To identify intervals with precision, intervals have a quality identifier.
Qualities of intervals can be one of them:
- Perfect
- Major
- Minor
- Augmented
- Diminished
- Doubly diminished
- Doubly augmented
But all intervals can't be identified with some of all identifiers, here are all possibilities:
| Major | Minor | Perfect | Augmented | Diminished | Doubly augmented | Doubly diminished | |
| Unison | |||||||
| Second | |||||||
| Third | |||||||
| Fourth | |||||||
| Fifth | |||||||
| Sixth | |||||||
| Seventh | |||||||
| Octave |
Below is the same table but classified to be more clear:
| Major | Minor | Perfect | Augmented | Diminished | Doubly augmented | Doubly diminished | |
| Unison | |||||||
| Octave | |||||||
| Fourth | |||||||
| Fifth | |||||||
| Second | |||||||
| Third | |||||||
| Sixth | |||||||
| Seventh |
Only unisons, fourths, fifths and octaves can be perfects but never major or minor.
Only seconds, thirds, sixths and sevenths can be major or minor but never perfects.
Intervals qualities in the C Major scale
Starting from the first note of the C Major scale, all intervals are only Majors or Perfects

| C - C | Unison | Perfect |
| C - D | Second | Major |
| C - E | Third | Major |
| C - F | Fourth | Perfect |
| C - G | Fifth | Perfect |
| C - A | Sixth | Major |
| C - B | Seventh | Major |
| C - C | Octave | Perfect |
You should keep in mind that in all Major scales, from the first note of the Major scale, all intervals are only Majors or Perfects.
Augmented and diminished intervals

- When a half step 

- When a half step is removed to a major interval, it results in a diminished interval
- When a half step is added to a perfect interval, it results in an augmented interval
- When a half step is removed to a perfect interval, it results in a diminished interval
- When a half step is added to an augmented interval, it results in a doubly augmented interval
- When a half step is removed to a diminished interval, it results in a doubly diminished interval
Examples of augmented and diminished intervals

Examples of minors, majors, augmented and diminished intervals

How to find interval name and quality?
For example, let's consider the interval C - B♭ :
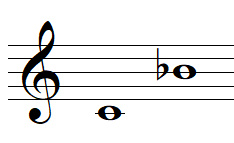
C D E F G A B = 1 2 3 4 5 6 7 = Seventh
The name of the interval C - B♭ is Seventh.
Now we will find the quality of this interval:
We know that from the first note of the C Major scale, all intervals are only Majors or Perfects and that only seconds, thirds, sixths and sevenths can be majors or minors but never perfects...
So the interval C - B♮ is a seventh major, so the interval C - B♭ is a seventh minor!

That's all! Easy no?
Numbers of whole steps (tones) in intervals
List of intervals according to the number of whole steps (tones):
| Major | Minor | Perfect | Augmented | Diminished | Doubly augmented | Doubly diminished | |
| Unison | 0 | ||||||
| Second | 1 | 0.5 | 1.5 | 2 | |||
| Third | 2 | 1.5 | 2.5 | 1 | 3 | 0.5 | |
| Fourth | 2.5 | 3 | 2 | 3.5 | 1.5 | ||
| Fifth | 3.5 | 4 | 3 | 4.5 | 2.5 | ||
| Sixth | 4.5 | 4 | 5 | 3.5 | 5.5 | 3 | |
| Seventh | 5.5 | 5 | 6 | 4.5 | 6.5 | 4 | |
| Octave | 6 |
Enharmonic
Two notes are enharmonic when they are tuning the same pitch, but spelled or named differently, examples:

Inversion of intervals
An interval can be inverted by raising the lower pitch an octave or lowering the upper pitch an octave, example:


unison become octave
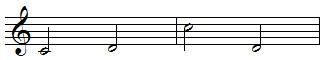
second become seventh

third become sixth
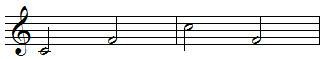
fourth become fifth
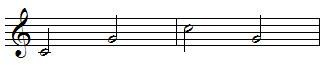
fifth become fourth
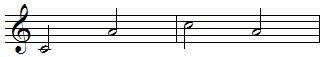
sixth become third
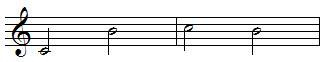
seventh become second
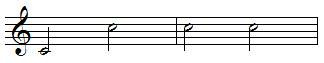
octave become unison
During inversions, intervals qualities change like this:
- Diminished intervals become augmented
- Minors intervals become majors
- Majors intervals become minors
- Augmented intervals become diminished
- Perfects intervals stay perfects
Compound intervals
A compound interval is an interval greater than one octave:

The quality of a compound interval is the same as the corresponding simple interval.
Intervals in the chromatic scale
Each notes of the chromatic scale are separated by a harf step interval (semitone), which can be either diatonic or chromatic:
Here is the ascending chromatic scale played on the piano:

And the descending chromatic scale:
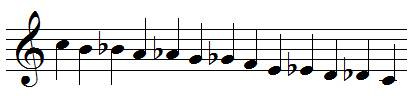
Reminder :
- A half step is chromatic when the two notes have the same name (C / C♯)
- A half step is diatonic when the two notes do not have the same name (C / D♭)
Liste of intervals
Perfect unison
Major second
Minor second
Augmented second
Doubly augmented second
Major third
Minor third
Augmented third
Diminished third
Doubly augmented third
Doubly diminished third
Perfect fourth
Augmented fourth
Diminished fourth
Doubly augmented fourth
Doubly diminished fourth
Perfect fifth
Augmented fifth
Diminished fifth
Doubly augmented fifth
Doubly diminished fifth
Major sixth
Minor sixth
Augmented sixth
Diminished sixth
Doubly augmented sixth
Doubly diminished sixth
Major seventh
Minor seventh
Augmented seventh
Diminished seventh
Doubly augmented seventh
Doubly diminished seventh
Perfect octave
External links :
1 - https://www.dolmetsch.com/musictheory12.htm
2 - https://en.wikipedia.org/wiki/Interval_(music)




